Dans son livre Fractales, hasard et finance le mathématicien Benoît Mandelbrot utilise un objet en or naturellement sculpté nommé le « buisson d’or » en image de couverture. Ce magnifique objet de la nature, conservé au Muséum national d’Histoire naturelle à Paris, fut désigné par Benoît Mandelbrot comme une illustration naturelle suffisamment parfaite des fractales. Désormais, plus d’une décennie après la mort du mathématicien, l’utilisation des fractales demeure restreinte dans le monde scientifique ou littéraire. Pourtant, l’utilité des fractales en tant qu’outil mathématique dans la prévision et les décisions d’investissement est absolument considérable. Après avoir présenté le concept de fractales dans cet article, on s’intéressera à la question de savoir si le cours de l’or est effectivement ou non dépendant du temps. En d’autres termes, si les tendances observées sur le cours de l’or sont explquées par le seul moment où elles se manifestent. Le cas de l’or est extrêmement intéressant car, au-delà de la symbolique voulue par Benoît Mandelbrot, les fractales sont très pertinentes en matière d’étude du cours de l’or.

Dans cet article, nous montrerons que le cours de l’or se comporte d’une manière indépendante a temps.

Source image : Le Buisson d’or | Muséum national d'Histoire naturelle (mnhn.fr)

Comprendre les fractales

Les fractales sont souvent mal comprises du public. Cela peut s’expliquer par le simple fait qu'elles illustrent un concept nouveau et récent dans l’histoire. Néanmoins, la compréhension des fractales chez le public reste souvent limitée par la complexité des explications des scientifiques et des spécialistes. Malgré tout, les fractales peuvent être définies assez simplement. En mathématiques, comme nous l’exposerons ici, les fractales se résument à une « simple » division.

Dans la finance, les fractales désignent la répétition de schémas de prix similaires sur des échelles de temps graduellement plus grandes ou plus petites. Par exemple, si une vague haussière est composée de trois sommets ascendants et de deux sommets descendants sur le cours d’une journée, alors il est tout à fait possible d’assister à la répétition de ce même schéma sur une décennie.

Les fractales sont intimement liées aux cycles qui ont fondé la réflexion et les recherches de Benoît Mandelbrot. Un actif sur lequel la cyclicité des cours est forte sera également un actif pour lequel les fractales seront marquées (la répétition des schémas de prix sera grande). Une fois que l’on a saisi cela, on peut dire dans une certaine mesure que les fractales sont l’expression d’un ordre constant dans le temps. Les fractales naissent d’une amplification (ou d’une réduction) entre les mouvements observés sur une échelle de temps plutôt courte et les mouvements à l’œuvre sur une échelle de temps plus longue.

Exemple de la fractale de Mandelbrot (répétition de figures graphiques) : Définition | Fractale | Futura Sciences (futura-sciences.com)

Une fois que cette définition est posée il est bien plus facile d’appréhender les fractales. En mathématiques, le degré fractal d’un actif se mesure à l’aide du coefficient de Hurst (compris entre 0 et 1). Ainsi :

• Si l’exposant de Hurst est égal à 0,5 ; alors le cours de l’or progresse de manière indépendante au temps qui s’écoule (le cours de l’or n’est pas fractal).
• Si l’exposant de Hurst est supérieur à 0,5 (et surtout 0,6) ; alors le cours de l’or progresse de manière dépendance et amplifiée au temps qui s’écoule (l’actif est fractal).
• Inversement, un exposant de Hurst inférieur à 0,5 (surtout 0,4) ; alors le cours de l’or progresse de manière dépendante et réduite au temps qui s’écoule (l’actif est fractal, mais plus difficilement lisible).

Mesure de la volatilité (historique) du cours de l’or

Nous avons d’abord calculé la volatilité sur une base mensuelle du cours de l’or afin de calculer la sensibilité du cours de l’or aux fractales. L’échantillon de données s’étale de janvier 2000 à septembre 2022, c’est-à-dire l’équivalent d’une période de 261 mois.

A l’aide du calcul de la volatilité (lire plus), nous obtenons que la volatilité mensuelle du cours de l’or entre janvier 2000 et septembre 2022 est de 4,72 %. De plus, la performance mensuelle moyenne du cours de l’or est de +0,84 %. Ces données à notre disposition sont indispensables à la mesure des fractales. Démarrons alors notre analyse sans porter attention à tous les aspects techniques…

Si le cours de l’or n’est pas sujet aux fractales, alors on peut utiliser les probabilités pour imaginer quelle sera la volatilité annuelle de l’or. En effet, l’hypothèse de Benoît Mandelbrot qui fonde la découverte des fractales est de faire l’hypothèse (en mathématiques) de non-stationnarité. C’est-à-dire que la distribution des variations du cours de l’or dans le passé est indépendante du temps dans le présent. Mais cela ne correspond à rien de véritable dans le monde réel…

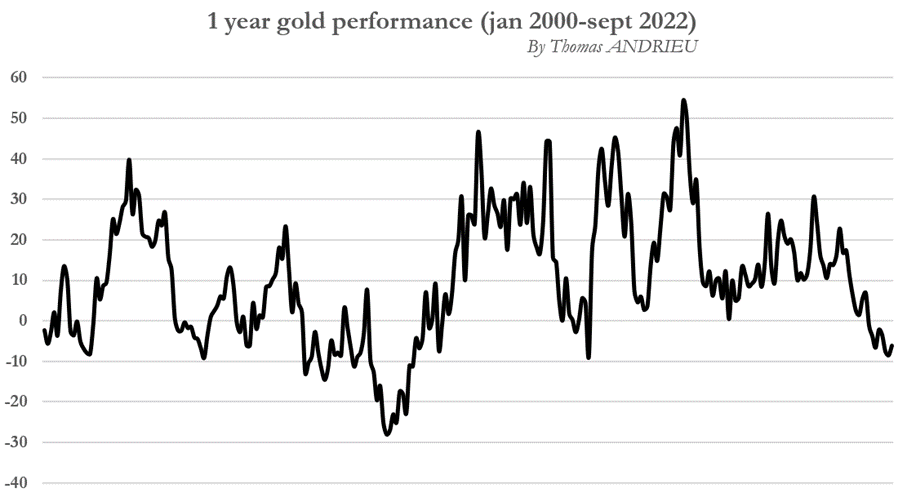
Dès lors, on cherche à calculer la volatilité annuelle (théorique) du cours de l’or en faisant l’hypothèse que l’évolution du cours de l’or est indépendant du temps (on annualise la volatilité selon la théorie des probabilités stationnaires). On obtient alors que la volatilité annuelle (théorique) du cours de l’or est de 16,35 % entre janvier 2000 et septembre 2022. A titre d’illustration, on a représenté ci-dessous la performance sur un an du cours de l’or entre 2000 et 2022. Le dernier record majeur de performance a été établi en 2006. Depuis cette date, nous sommes entrés dans un nouveau cycle de chute des performances de l’or qui pourrait se terminer bientôt.

Pour la parenthèse technique, on a mentionné le détail (facultatif) du calcul ci-dessous. On multiplie la volatilité mensuelle observée par la racine du nombre de mois dans une année pour obtenir la volatilité annualisée. Le paramètre déterminant dans cette équation est l’exposant ½ (qui est en vérité l’exposant de Hurst), c’est lui qui définit les fractales d’un actif. Mais on pose ici ½ d’après l’hypothèse de stationnarité, nous y reviendrons plus loin…

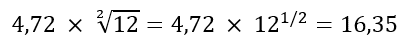
Or et fractales

Désormais, il nous suffit de mesurer la volatilité annuelle effectivement observée pour enfin savoir si le cours de l’or est dépendant du temps sur une échelle de moyen terme. Sur la période janvier 2000 à septembre 2022, la volatilité historique annualisée observée est de 16,8 %. Elle est donc différente (de peu) de la volatilité théorique calculée de 16,35 %. Comme l’écart entre la volatilité théorique et la volatilité observé est faible, on peut s’attendre à ce que les fractales soient peu influentes à moyen terme (le coefficient de Hurst est proche de 0,5).

Dans le détail du calcul (facultatif), on cherche à résoudre l’équation qui nous permet d’obtenir la valeur de H, c’est-à-dire l’exposant qui transforme la véritable volatilité mensuelle en volatilité annuelle. En reprenant la formule générale énoncée par Benoît Mandelbrot, à savoir ln(P)/ln(t) où P est la variation des prix d'une période sur l'autre et où t est le temps écoulé, on obtient que la valeur de H est de 0,51.

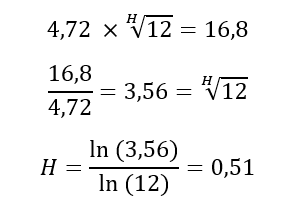
En conséquence, le coefficient de Hurst qui mesure le degré fractal d’un actif est relativement très proche de 0,5. Cela signifie assez clairement que l’évolution du cours de l’or est relativement indépendante ou presque de l’écoulement du temps. Mais peut-on globalement affirmer que l’or n’est pas sensible aux cycles et à l’évolution du temps ?...

L’importance des échelles de temps…

Mais pour l’écrire ainsi… L’or n’a pas dit son dernier mot. Si l’or est indépendant du temps à moyen terme (de l’échelle mensuelle à l’échelle annuelle), ce n’est pas mécaniquement le cas pour les autres échelles de temps. On a appliqué la même méthodologie en utilisant rigoureusement les données hebdomadaires du cours de l’or entre janvier 2000 et septembre 2022.

La volatilité hebdomadaire de l’or mesurée entre janvier 2000 et septembre 2022 est de 2,32 %... En conséquence, il nous est possible de savoir si le cours de l’or est sensible au temps entre une échelle hebdomadaire et une échelle mensuelle, ou encore une échelle hebdomadaire et une échelle annuelle. Pour ce faire, nous appliquons le même calcul expliqué dans la partie précédente. Ainsi, on obtient les résultats suivants :

• La valeur de H entre un échantillon hebdomadaire et un échantillon annuel est de 0,501 (ln7,24/ln52).
• La valeur de H entre un échantillon hebdomadaire et un échantillon annuel est de 0,51 (ln2,03/ln4).

En conséquence, qu’il s’agisse de l’or sur le cours terme ou sur le long terme, sa trajectoire est relativement indépendante du temps. Ce qui est assez rare pour être remarqué sur les marchés financiers… Mais nous devons garder ceci à l’esprit : le degré fractal d’un actif est variable au cours du temps, et les calculs réalisés nous donnent une sorte de moyenne de l’ensemble des coefficients passés. Par exemple, le coefficient de Hurst était globalement inférieur à 0,5 en 2015, ce qui laissait présager un retournement haussier futur (le cours de l’or était réduit avec les échelles de temps plus longues, ce qui n’est pas la norme pour le métal jaune).

Aussi, il est important de spécifier qu’avant 2000, le cours de l’or possédait un coefficient de Hurst supérieur à 0,5 (proche de 0,6 dans les années 1980, ce que l’on peut notamment lire dans certains travaux de Benoît Mandelbrot). Le fait que l’évolution du prix de l’or soit devenue relativement indépendante au temps est un phénomène relativement récent (depuis les années 2000) et démontre la grande stérilité de l’or à générer des ajustements de marchés différents à court terme ou à long terme…

L’exemple du bitcoin (BTC)

Le cas du bitcoin (BTC) est très intéressant dans la mesure où il est l’antithèse absolue de l’or. En effet, le coefficient de Hurst mesuré entre l’évolution mensuelle et l’évolution annuelle de l’or est de 0,92 (lire plus). C’est-à-dire que le bitcoin (BTC) est entièrement dépendant ou presque de la temporalité, et que les probabilités stationnaires sont largement inefficaces pour décrire son évolution dans le temps. Ce qui explique les tendances de prix sur cryptomonnaies, c’est le moment où ces tendances apparaissent… En ce sens, le bitcoin s’oppose au cours de l’or qui se montre indépendant des risques liés à la temporalité des évènements.

Il est assez notable de remarquer généralement que les actifs les plus volatils sont aussi les actifs les plus dépendants de la temporalité des tendances. L’or est donc un actif à priori détaché du temps qui n’a pas ou peu d’influence sur son évolution.

En conclusion

Nous avons montré que les fractales étaient un moyen très pertinent de mesurer le véritable comportement d’un actif. La seule existence (ou absence) de fractales sur le cours d’un actif financier permet de juger si le cours de l’actif est dépendant (ou indépendant) du temps qui s’écoule. Dans ses ouvrages, Benoît Mandelbrot parler « d’auto force relative » pour parler des fractales. C’est la capacité d’un actif à amplifier ou à réduire ses tendances passées. Cela traduit la présence de cycles plus marqués sur le cours de l’actif en question.

Le cas de l’or, symboliquement choisi par l’auteur des fractales, est un cas absolument intéressant. On avait l’habitude de lire dans le passé (autour des années 1980 et jusqu’à la fin du siècle) que le cours de l’or était un actif dépendant du temps, au même titre que les actions ou plusieurs autres métaux. Mais l’étude rigoureuse des données dont nous disposons démontre à l’inverse que l’or est devenu, depuis 2000, un actif temporellement stérile. Qu’il s’agisse des échelles de temps courtes, ou des échelles de temps de moyen terme, l’or montre une insensibilité au temps… Cela n’empêche pas la présence de cycles, mais ils deviennent plus difficiles à lire.

Mais alors comment expliquer cette stérilité du cours de l’or face aux effets du temps ? Et comment justifier que l’or est invariable avec le temps, et que sa stabilité est digne de la théorie élémentaire la plus parfaite ?

Puisque les fractales ne sont que d’une moindre utilité dans la lecture du cours de l’or, il est légitime de chercher des explications ailleurs, mais les réponses à cette question demeurent complexes et on ne peut y répondre à ce jour… Il y a quelque chose de fascinant dans le cours de l’or : cette capacité à être stable face à toutes les épreuves du temps, ce qu’une infime proportion des actifs de cette planète sont en capacité d’assurer à ce jour. Malgré le fait que le cours de l’or est assurément moins cyclique que d’autres actifs, on ne peut que se réjouir à l’observation que ses performances sont biaisées à la hausse.